Here I show how to price a simple GMDB (unit linked insurance product) using installment options and calculate the premium using a binominal tree approach. The analysis shows that non-rational policy holder behaviour leads to strong mispricing.
Contents
Variable annuities (VAs) are unit linked insurance products often embedding financial options and guarantees (for an overview on VA products see e.g. Ledlie et al.). The price of these embedded options are not - like in traditional over the counter or exchange traded derivative securities - paid in advance but by installment as a proportional fee of the unit account.
We will give a very short introduction to standard installment options. Then we will price a simplified VA product - a guaranteed minimum maturity benifit (GMMB) - using an online calculator (see also Introduction to Option Pricing Using Binomial Trees ). We will look at the prices when assuming full rational behaviour (arbitrage free view) and no rational behaviour.
A standard installment options (deferred premium option) is a European option in which the premium is paid in a series of payments instead of being payed up-front. The holder has the right to terminate payments on any installment date in which case the option lapses with no further payments on both sides (definition taken from Davis et al.). Let us consider an installment call with maturity $T=t_2$ and premium payments $p_0$ at $t_0$ and $p_1$ at $t_1$. As Davis et al. point out, an installment call can be seen as the underlying vanilla call with premium payments $p_0$, $p_1$ plus the right to sell the call option at $t_1$ for $p_1$. Thus the price for the installment call option is the sum of the price for the vanilla call and the price for a put on the call with strike $p_1$ and maturity $t_1$. Therefore the price for an installment option is higher than the Black-Scholes-Price on the underlying vanilla option.
To price the initial premium $p_0$ for an installment put option given the equal installment premiums $p_1=\cdots=p_n$ in the Cox-Ross-Rubinstein binomial tree model we use the following procedure starting at the rightmost leaf nodes:
At the leave nodes the price resp. payoff is \begin{equation} V_n=\max(K-S_T,0) \end{equation}
At inner nodes $i$ where $t_i$ matches an installment date the holder lapses when the premium $p_i$ is greater the current option value. So the price is given by \begin{equation} V_i=\max\left[0, e^{-r\Delta t}\left(pV_{i+1}^{up}+(1-p)V_{i+1}^{down}\right) - p_i\right]. \end{equation}
At any other node $i$ the price is \begin{equation} V_i=e^{-r\Delta t}\left(pV_{i+1}^{up}+(1-p)V_{i+1}^{down}\right) \end{equation}
In the above formulation $K$ is the strike price, $S$ is the price of the underlying stock in the respective state and time step $t_i$, $p$ and $(1-p)$ is the probability of an up resp. down movement and $V_{i+1}^{up }$ and $V_{i+1}^{down}$ is the option value at time $t_{i+1}$ for an up resp. down movement (for more details on binomial trees please refer to Introduction to Option Pricing Using Binomial Trees or any text book on financial options like John C. Hull).
As we see, the installment options has an American-style way of valuation (the holder of an American option has the right to exercise at any time; he exercises only when the payoff is greater than the option value). It is clear, that an installment option cannot be evaluated using a standard Monte-Carlo-Scheme, since - as with American options - we need the option value at future dates.
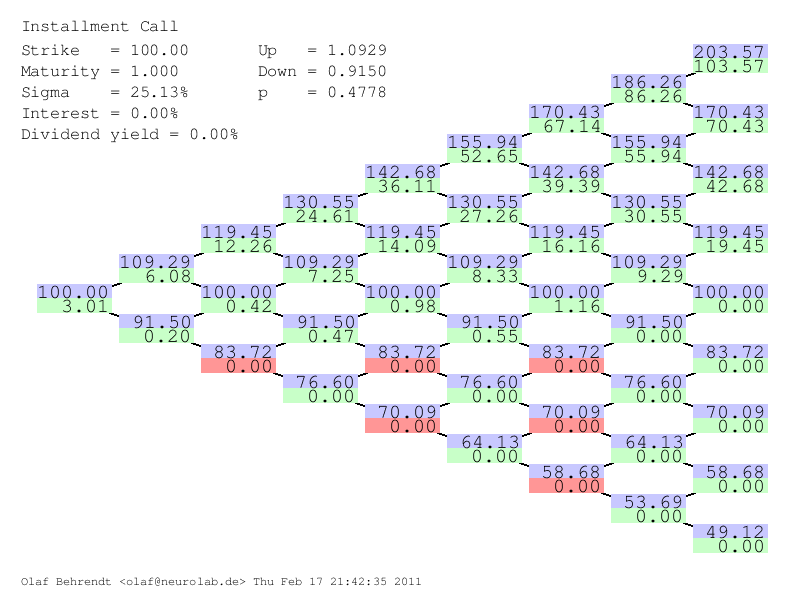
Let us calculate a simple example taken from Davis et al. where $T$=1 year, $r$=0, $K$=100, $S_0$=100, $\sigma$=25.132% and four equal installments of $p_i$=3.284 at $t_0$=0, $t_1$=0.25, $t_2$=0.5 and $t_3$=0.75. Using 5000 time steps we calculate $p_0$=3.28184 (Davis et al. calculated 3.284, the difference might stem from the fact that the online calculator is based on four byte floats and not on eight byte doubles). The present value of all installment premiums is 13.13384. When we assume an investor who never lapses (a non-rational investor) the present value of all installment premiums equals the Black-Scholes price which is approx. 10 (9.999911).
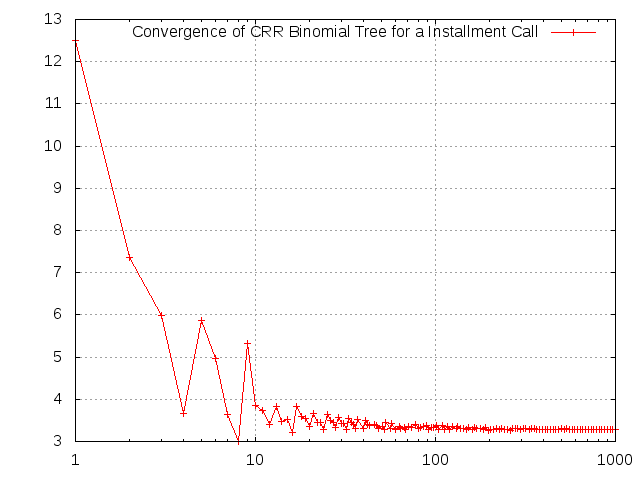
In order to visualize the tree we also perform a calculation using only 8 time steps. Then we calculate values to visualize the convergence of the tree.

Our simplified GMMB has the following properties:
So at time zero the policy holder pays 100 into his unit account. After ten years he receives the maximum of his unit account and his single premium (100). This obviously is a kind of installment put, where the installment payments are a percentage of the underlying investment and is deducted from it (which can be viewed as a kind of dividend). To evaluate such a derivative we only need to make some small changes to the binomial tree algorithm outlined above as sketched below.
At the leave nodes the price is \begin{equation} V_n = \max(K-S_T,0) \end{equation}
At inner nodes $i$ where $t_i$ matches an installment date the account value is reduced by the guarantee fee (we assume payment in advance): $S_i^+=S_i^-(1-q)^{\Delta t}$. The installment premium $p_i = S_i^--S_i^+=S_i^-\left(1-(1-q)^{\Delta t}\right)$ and \begin{equation} V_i=\max\left[0, e^{-r\Delta t}\left(pV_{i+1}^{up}+(1-p)V_{i+1}^{down}\right) - p_i\right]. \end{equation}
At any other node $i$ the price is \begin{equation} V_i=e^{-r\Delta t}\left(pV_{i+1}^{up}+(1-p)V_{i+1}^{down}\right) \end{equation}
Comparing the above algorithm with the algorithm for the "plain vanilla" installment option we see that we only changed the development of the underlying asset (from which the guarantee fee is financed) and the calculation of installment payments $p_i$.
$T$=10, $r$=3%, $K$=100, $S_0$=100, $\sigma$=20%, monthly guarantee payment ($\Delta t = 1/12$):
Rational investor: Guarantee fee $q$ = 4.584%
Non-rational investor: Guarantee fee $q$ = 1.554%
For our simplified GMMB there is a significant difference between the price assuming a rational investor versus the price assuming a non-rational investor. Introducing ratchets in our product where ratchet dates are identical to the installment premiums would certainly result in an identical price for any investor type. In practice the ratchet dates are often yearly and premium payments are on a monthly base which would again introduce a higher price for a rational investor. It would be interesting to expand our study to a GMMB with ratchets.